Tabla trigonométrica completa Sin Cos Tan (todos los ángulos) + Cómo entenderla

La tabla trigonométrica sin cos tan es una serie de tablas que contienen el valor trigonométrico o sin cos tangente de un ángulo.

En este artículo, se muestra una tabla de valores trigonométricos para sin cos tan desde varios ángulos especiales desde el ángulo de 0º a 360º (o lo que comúnmente se llama el ángulo del círculo de 360 grados), para que no tenga que molestarse en memorizarlos más.

En cuanto a la fórmula de identidad trigonométrica, puedes leerla en este artículo.

Definición de Sin Cos Tan

Antes de entrar en la tabla de valores trigonométricos, es una buena idea comprender primero los términos trigonometría y sin cos tan.

La trigonometría es una rama de las matemáticas que estudia la relación entre la longitud y el ángulo de un triángulo.
Sin (seno) es la razón de la longitud en un triángulo entre el frente del ángulo y la hipotenusa, y / z.
Cos (coseno) es la razón de la longitud en un triángulo entre el lado del ángulo y la hipotenusa, x / z.
Tan (tangente) es la razón de las longitudes en un triángulo entre el frente de la esquina y el lado, y / x.

Todas las comparaciones trigonométricas de tan sin cos están limitadas a ser válidas solo para triángulos rectángulos o triángulos con un ángulo de 90 grados.

Tabla de trigonometría de ángulo especial del cuadrante I (0 - 90 grados)

Esquina	0 º	30 º	45 º	60 º	90 º
Pecado	0	1/2	1/2 √2	1/2 √3	1
Porque	1	1/2 √3	1/2 √2	1/2	0
Broncearse	0	1/2 √3	1	√3	∞

Tabla de trigonometría del cuadrante de ángulo especial II (90 - 180 grados)

Esquina	90 º	120 º	135 º	150 º	180 º
Pecado	1	1/2 √3	1/2 √2	1/2	0
Porque	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
Broncearse	∞	-√3	-1	- 1/3 √3	0

Cuadrante de ángulo especial III de la tabla Sin Cos Tan (180 - 270 grados)

Esquina	180 º	210 º	225 º	240 º	270 º
Pecado	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
Porque	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
Broncearse	0	1/3√3	1	√3	∞

Tabla de Cos Sin Tan Cuadrante de ángulo especial IV (270 - 360 grados)

Esquina	270 º	300 º	315 º	330 º	360 º
Pecado	-1	-½√3	-½√2	-½	0
Porque	0	½	½√2	½√3	1
Broncearse	∞	-√3	-1	-1 / 3√3	0

Por lo tanto, una lista completa de tablas trigonométricas de todos los ángulos especiales de 0 a 360 grados.

Lea también: Proceso del mecanismo de visión humana y consejos para el cuidado de los ojos

Puede utilizar esta tabla para facilitar los negocios en el cálculo o análisis de trigonometría en matemáticas.

Recuperación de la tabla trigonométrica de ángulo especial sin memorización

De hecho, no tiene que molestarse en memorizar todos los valores trigonométricos desde todos los ángulos.

Todo lo que necesita es un concepto básico de comprensión que puede utilizar para averiguar el valor trigonométrico de cualquier ángulo en particular.

Solo necesita recordar los componentes de la longitud de los lados del triángulo en ángulos especiales de 0, 30, 45, 60 y 90 grados.

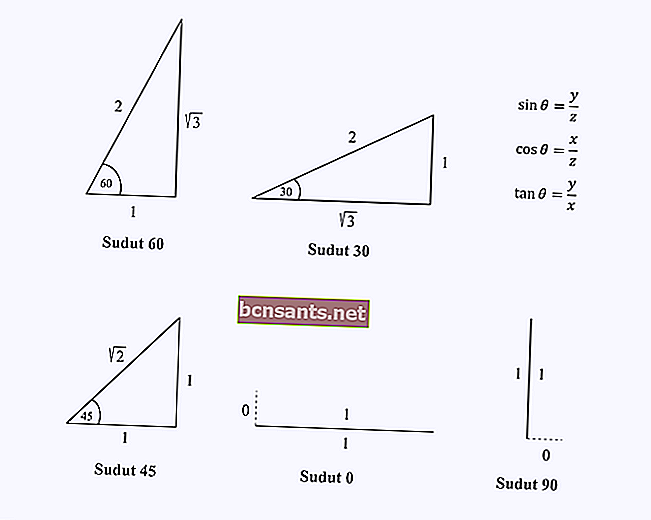
Suponga que desea encontrar el valor de cos (60).

Solo necesita recordar la longitud del lado del triángulo con un ángulo de 60 grados, luego realice la operación del coseno, que es x / z en ese triángulo.

En la figura, verá que el valor de cos 60 = 1/2.

Fácil ¿verdad?

Para los ángulos en los otros cuadrantes, el método es el mismo y solo necesitas ajustar el signo positivo o negativo de cada cuadrante.

Mesa en forma de círculo

Si la tabla de cosen tan de arriba es demasiado larga para recordarla, también si el método del concepto de ángulo especial que cree que todavía es difícil ...

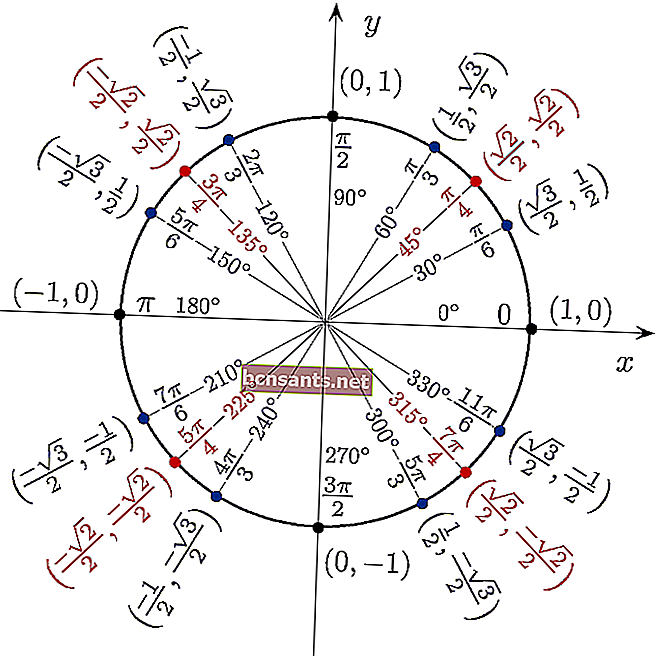
Puede utilizar la tabla trigonométrica en forma de círculo para ver directamente el valor de sin cos tan desde un ángulo de 360 grados.

Trucos rápidos para memorizar tablas trigonométricas

Aparte de los métodos anteriores, todavía hay un método más que puede utilizar para recordar fácilmente tablas de fórmulas trigonométricas.

Los pasos que debe seguir son los siguientes:

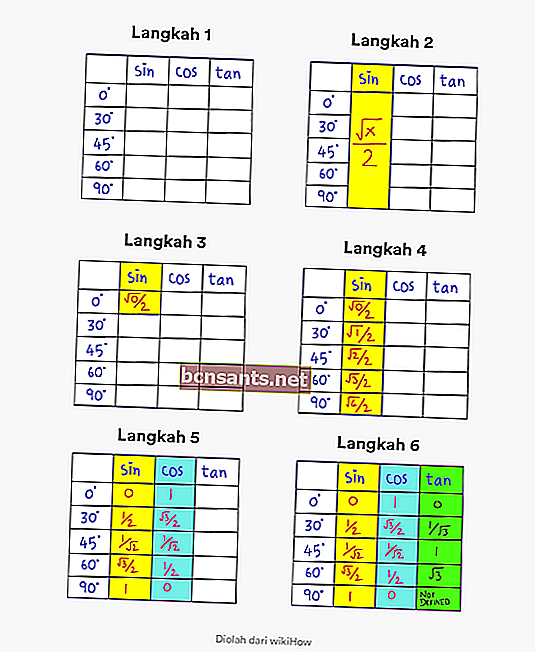
Paso 1 . Cree una tabla que contenga ángulos de 0 a 90 grados y columnas con la descripción sin cos tan
Paso 2 . Tenga en cuenta que la fórmula general para el pecado en un ángulo de 0 a 90 grados es √x / 2.
Paso 3 . Cambie el valor de x a 0 en √x / 2 en la primera columna. Esquina superior izquierda.
Paso 4. Complete la secuencia cambiando x a 0, 1, 2, 3, 4 en la columna sin. Así tienes el valor trigonométrico completo sin
Paso 5 . Para encontrar el valor de cos, todo lo que necesita hacer es invertir el orden en la columna sin.
Paso 6 . Para encontrar el valor de bronceado, todo lo que necesita hacer es dividir el valor del pecado por el valor del cos.

Lea también: Historias de ficción: ejemplos, definición y elementos [COMPLETO

Cómo memorizar la tabla trigonométrica sin cos tan

¿Cuál es más fácil de entender para recordar el valor trigonométrico de tan sin cos?

De cualquier manera, elija la que le resulte más fácil de entender. Porque cada persona tiene un estilo de aprendizaje diferente.

Tablas para todos los ángulos

Si en las tablas anteriores los valores mostrados son solo los valores trigonométricos de ángulos especiales, entonces esta tabla muestra todos los valores trigonométricos de todos los ángulos de 0 a 90 grados.

Esquina	Radianes	Pecado	Porque	Broncearse
0 °	0	0	1	0
1 °	0.01746	0.01746	0.99985	0.01746
2 °	0.03492	0.03491	0,99939	0.03494
3 °	0.05238	0.05236	0,99863	0.05243
4 °	0.06984	0.06979	0,99756	0.06996
5 °	0.0873	0.08719	0.99619	0.08752
6 °	0.10476	0.10457	0,99452	0.10515
7 °	0.12222	0.12192	0,99254	0.12283
8 °	0.13968	0.13923	0.99026	0.1406
9 °	0.15714	0,1565	0,98768	0.15845
10 °	0,1746	0.17372	0,9848	0,1764
11 °	0.19206	0.19089	0.98161	0.19446
12 °	0.20952	0.20799	0,97813	0.21265
13 °	0.22698	0.22504	0.97435	0.23096
14 °	0.24444	0.24202	0,97027	0.24943
15 °	0.26191	0.25892	0,9659	0.26806
16 °	0.27937	0.27575	0.96123	0.28687
17 °	0.29683	0.29249	0,95627	0.30586
18 °	0.31429	0.30914	0,95102	0.32506
19 °	0.33175	0.32569	0,94548	0.34448
20 °	0.34921	0.34215	0.93965	0.36413
21 °	0.36667	0.35851	0.93353	0.38403
22 °	0.38413	0.37475	0.92713	0.40421
23 °	0.40159	0.39088	0,92044	0.42467
24 °	0.41905	0.40689	0,91348	0,44543
25 °	0.43651	0.42278	0.90623	0.46652
26 °	0.45397	0.43854	0.89871	0.48796
27 °	0.47143	0.45416	0.89092	0.50976
28 °	0.48889	0,46965	0.88286	0.53196
29 °	0.50635	0.48499	0.87452	0.55458
30 °	0.52381	0.50018	0.86592	0.57763
31 °	0.54127	0.51523	0.85706	0,60116
32 °	0.55873	0.53011	0.84793	0,62518
33 °	0.57619	0.54483	0.83854	0,64974
34 °	0.59365	0.55939	0.8289	0,67486
35 °	0,61111	0.57378	0.81901	0,70057
36 °	0,62857	0.58799	0,80887	0,72693
37 °	0,64603	0,60202	0,79848	0,75396
38 °	0,66349	0,61587	0,78785	0,78172
39 °	0,68095	0.62953	0,77697	0.81024
40 °	0,69841	0,643	0,76586	0.83958
41 °	0,71587	0,65628	0,75452	0.86979
42 °	0,73333	0,66935	0,74295	0.90094
43 °	0,75079	0,68222	0,73115	0.93308
44 °	0,76825	0,69488	0,71913	0,96629
45 °	0,78571	0,70733	0,70688	1,00063
46 °	0,80318	0,71956	0,69443	1.0362
47 °	0,82064	0,73158	0,68176	1.07308
48 °	0.8381	0,74337	0,66888	1.11137
49 °	0.85556	0,75494	0,6558	1,15117
50 °	0.87302	0,76627	0,64252	1.1926
51 °	0.89048	0,77737	0.62904	1,2358
52 °	0.90794	0,78824	0,61537	1.28091
53 °	0.9254	0,79886	0,60152	1.32807
54 °	0,94286	0,80924	0.58748	1.37748
55 °	0,96032	0.81937	0.57326	1.42932
56 °	0.97778	0.82926	0.55887	1.48382
57 °	0,99524	0.83889	0.5443	1.54122
58 °	1.0127	0,84826	0.52957	1,60179
59 °	1.03016	0.85738	0.51468	1.66584
60 °	1.04762	0.86624	0,49964	1,73374
61 °	1.06508	0.87483	0.48444	1.80587
62 °	1.08254	0.88315	0.46909	1.8827
63 °	1.1	0.89121	0.4536	1,96476
64 °	1.11746	0.89899	0.43797	2.05265
65 °	1.13492	0.9065	0.4222	2.14707
66 °	1.15238	0.91373	0.40631	2.24884
67 °	1.16984	0,92069	0.3903	2.35894
68 °	1.1873	0.92736	0.37416	2.4785
69 °	1,20476	0.93375	0.35792	2.60887
70 °	1.22222	0.93986	0.34156	2.75169
71 °	1.23968	0,94568	0.3251	2.90892
72 °	1.25714	0,95121	0.30854	3.08299
73 °	1.2746	0.95646	0.29188	3.27686
74 °	1.29206	0.96141	0.27514	3,49427
75 °	1.30952	0.96606	0.25831	3.73993
76 °	1.32698	0,97043	0.2414	4.01992
77 °	1.34444	0.97449	0.22442	4.34219
78 °	1.36191	0.97826	0.20738	4.71734
79 °	1.37937	0.98173	0.19026	5.15984
80 °	1.39683	0.98491	0.1731	5.68998
81 °	1.41429	0.98778	0.15587	6.33709
82 °	1.43175	0.99035	0.1386	7.14523
83 °	1.44921	0,99262	0.12129	8.18379
84 °	1.46667	0,99458	0.10394	9.56868
85 °	1.48413	0.99625	0.08656	11,5092
86 °	1,50159	0,99761	0.06915	14,4259
87 °	1.51905	0,99866	0.05173	19.3069
88 °	1.53651	0.99941	0.03428	29,153
89 °	1.55397	0,99986	0.01683	59.4189
90 °	1.57143	1	0	∞

Con suerte, esta explicación trigonométrica puede serle de utilidad.

Este material será de gran utilidad para diversas aplicaciones en matemáticas y física avanzadas.

También puede aprender otros materiales escolares en Saintif, como números primos, conversiones de unidades, fórmulas rectangulares, etc.

Referencia

Trigonometría - Wikipedia
Herramientas matemáticas: trigonometría