
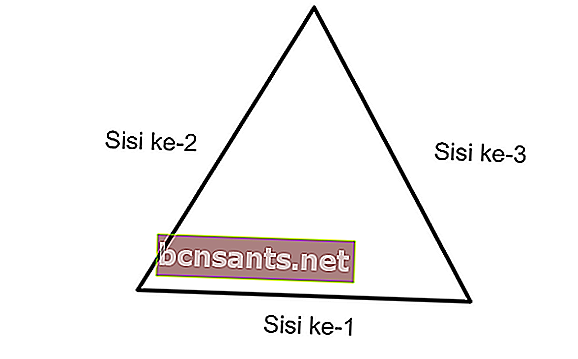
El perímetro del triángulo es la longitud total del lado del triángulo. Por lo tanto, la fórmula para el perímetro del triángulo es K = a + b + c o la suma de todos los lados del triángulo.
Cuando circulas alrededor del jardín triangular, ¿qué significa eso? ¡Sí! Estás rodeando una forma de triángulo. ¿Qué es una forma de triángulo plano? La siguiente es una explicación del triángulo, el tipo de triángulo y cómo determinar o la fórmula para el perímetro del triángulo.
Explicación del triángulo
Un triángulo es una forma formada por tres líneas que se cruzan y forman un ángulo. El número de ángulos en un triángulo es 180 grados.
Los triángulos son las formas planas más simples porque son elementos que forman otras formas planas como cuadrados, rectángulos, círculos y elementos de formas planas que forman formas como prismas y pirámides.
Características de un triángulo
Para explicar mejor el significado de un triángulo, dibujaré una forma de triángulo arbitraria ABC a continuación:
Los elementos del triángulo ABC incluyen:
- Los puntos A, B y C se conocen como vértices.
- Las rectas AB, BC y CA se denominan lados del triángulo.
- Los diversos triángulos se pueden ver desde las longitudes de los lados y los ángulos formados por el triángulo.
Tipos de triángulos
Los tipos de triángulos varían ampliamente según la longitud de los lados y ángulos que forman el triángulo. La siguiente es la división de los tipos de triángulos.
Tipos de triángulos según la longitud de los lados
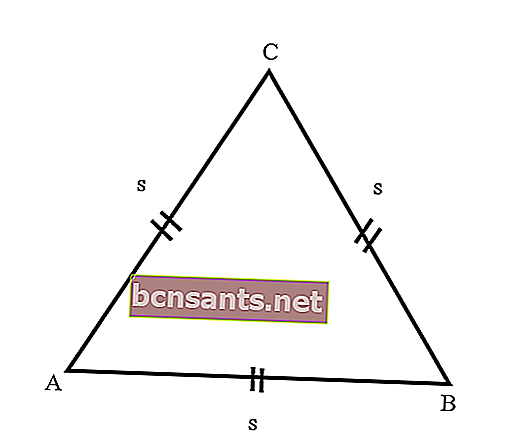
- Triángulo equilátero
Es decir, un triángulo con los tres lados de la misma longitud. Además, los tres ángulos formados por el triángulo lateral tienen el mismo tamaño, que es de 60 grados, porque el número de ángulos del triángulo es de 180 grados.
Para obtener más información sobre los triángulos equiláteros, considere la siguiente explicación de las propiedades de los triángulos equiláteros:

En la Figura (b) - (d) se puede ver que la forma del triángulo ABC puede ocupar su marco exactamente usando 3 formas, a saber, rotado hasta 120 grados centrado en el punto O (observe la dirección de rotación) en (Figura b) rotado hasta 240 grados en el centro de rotación en O (en la figura c) que se gira 360 grados (una vuelta completa) en el punto central en O (en la figura d).
Lea también: Fórmulas de oportunidad y ejemplos de problemasDe acuerdo con la explicación de las figuras a af, el triángulo equilátero ABC tiene simetría rotacional hasta el nivel 3. Mientras tanto, las figuras e, f y g invertidas pueden ocupar el marco correctamente. Para ello, la forma del triángulo ABC tiene 3 ejes de simetría. Mientras que en la imagen de arriba, los ejes de simetría son CD, BF y AE. De modo que el triángulo equilátero puede ocupar el marco exactamente de 6 maneras.
Basado en algunas de las descripciones anteriores, algunas de las propiedades que existen en un triángulo equilátero incluyen: tiene 3 niveles de simetría rotacional, 3 ejes de simetría, 3 lados equiláteros, 3 ángulos iguales de 60 grados y puede ocupar el marco de hasta 6 formas.
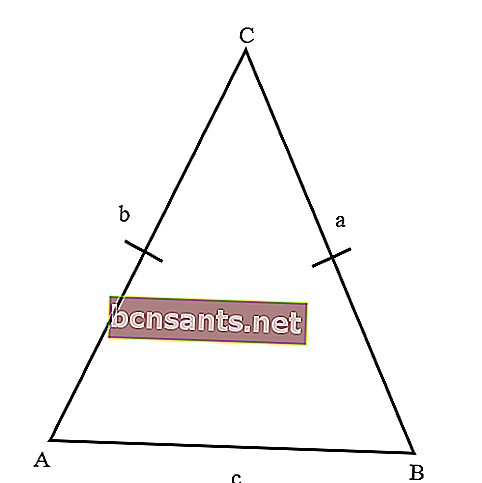
- Triángulo isósceles
Es decir, un triángulo con un lado de la misma longitud. Un triángulo isósceles tiene dos ángulos iguales, es decir, ángulos enfrentados.
Las siguientes son las propiedades del triángulo isósceles;
- La construcción de un triángulo isósceles, girado una vuelta completa, ocupa el marco exactamente de una manera. De modo que el triángulo samakaki tiene una simetría giratoria de uno.
- Mientras tanto, un triángulo isósceles tiene solo un eje de simetría.
- Cualquier triangulo
Es decir, un triángulo con tres lados que no tienen la misma longitud y los tres ángulos no son iguales.

Aquí están las propiedades de cualquier triángulo:
- Tiene tres lados que no tienen la misma longitud. (En la imagen de arriba, los tres lados deben tener la longitud BA ≠ CB ≠ AC).
- No tiene simetría de pliegue.
- Tiene solo una simetría giratoria.
- Las tres esquinas tienen diferentes tamaños.
Tipos de triángulos según el ángulo
- Triángulo agudo
Es decir, un triángulo con los tres ángulos formando un ángulo agudo. Un ángulo agudo es un ángulo que varía de 0 a 90 grados.
- Triángulo romo
Es decir, un triángulo con una esquina que forma un ángulo obtuso. Un ángulo obtuso es un ángulo cuya magnitud está en el rango de 90 a 180 grados.
Lea también: ¡Soluciones para fórmulas olvidadas a menudo!
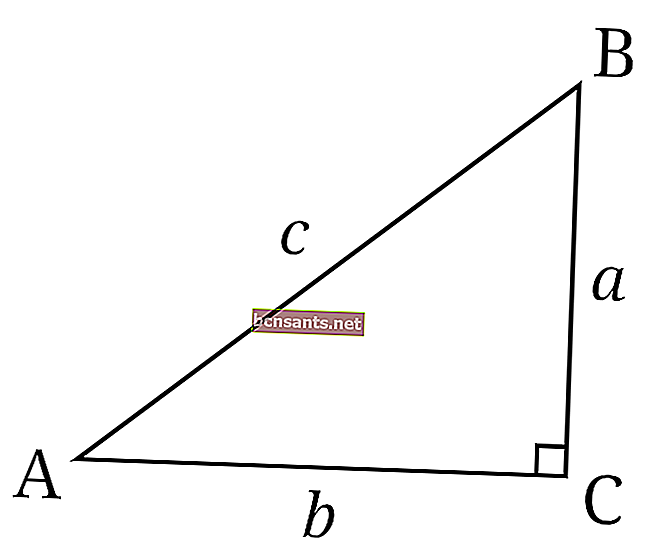
- Triángulo rectángulo
Es decir, un triángulo con una de las esquinas formando un ángulo de 90 grados.
La fórmula del perímetro de un triángulo
El perímetro de la forma se obtiene a partir del número de longitudes de los bordes (sisis) que forman la forma.
Entonces, la fórmula para el perímetro de un triángulo se puede obtener sumando cada lado del triángulo.
Perímetro del triángulo = longitud del primer lado + longitud del segundo lado + longitud del tercer lado
K = a + b + c
Problema de ejemplo para encontrar el perímetro de un triángulo
Problema de ejemplo 1.
Un triángulo equilátero tiene una longitud de lado de 3 cm, ¿cuál es la circunferencia?
Asentamiento:
Ya sabes: s = 3 cm
Se busca: ¿ perímetro del triángulo?
Responder:
Los triángulos equiláteros tienen los mismos lados,
K = s + s + s
K = 3 + 3 + 3
K = 9 cm
Entonces, el perímetro del triángulo equilátero es de 9 cm.
Problema de ejemplo 2.
Un triángulo isósceles tiene una longitud total de lado de 36 cm. El lado más largo mide 13 cm. ¿Cuál es la longitud del lado más corto?
Asentamiento:
Sabes que = K = 36 cm; b = a = 13 cm
Se busca : ¿La longitud del lado más corto?
Respuesta :
Perímetro del triángulo = a + b + c
36 = 13 + 13 + c
c = 10 cm
Entonces, la longitud del lado más corto del triángulo es de 10 cm
Problema de ejemplo 3.
Te dan cualquier triángulo con lados de 9, 11, 13 cm cada uno. ¡Calcula el perímetro del triángulo!
Asentamiento:
Se sabe que : a = 13 cm; b = 9 cm; c = 11cm
Se busca : ¿perímetro del triángulo?
Responder:
K = a + b + c
K = 13 +9 +11
K = 33 cm
Entonces, el perímetro del triángulo es 33 cm
Problema de ejemplo 4.
Calcula el perímetro del triángulo isósceles con un área de 12 cm2 y la longitud del lado de 6 cm.
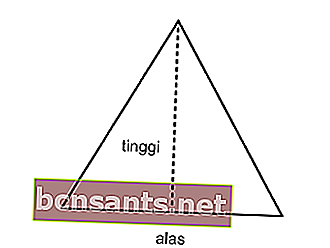
Asentamiento:
Ya sabes: L = 12 cm2; a = 6 cm
Se busca: ¿ perímetro del triángulo?
Responder:
Para encontrar el perímetro del triángulo, debes conocer la longitud de los lados del triángulo.
Usa el área para encontrar la altura del triángulo
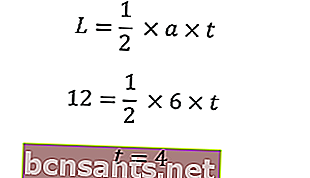
Usando el sistema de Pitágoras, conocemos la hipotenusa de un triángulo isósceles ingresando la longitud de la base (a) y la altura del triángulo (t)

Usando la ecuación anterior, obtenemos la hipotenusa del triángulo
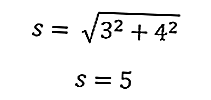
Esto te permitirá calcular el perímetro del triángulo inmediatamente.
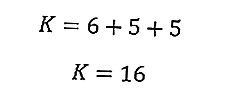
Entonces, el perímetro del triángulo es de 16 cm.
Referencia : Triángulo - Las matemáticas son divertidas
