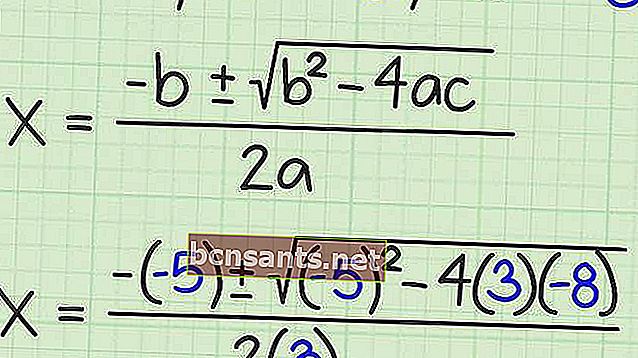
La fórmula ABC es una forma excelente de encontrar las raíces de varias formas de ecuaciones cuadráticas, incluso si el resultado no es un número entero.
La ecuación cuadrática ax2 + bx + c = 0 se puede resolver usando varios métodos. Entre ellos se encuentran el método de factorización, completando el cuadrado ABC y la fórmula.
Entre estos métodos, la fórmula abc es excelente porque se puede usar para encontrar las raíces de varias formas de ecuaciones cuadráticas incluso si el resultado no es un número entero.
La siguiente es una explicación más detallada de la fórmula, que incluye comprensión, preguntas y discusión.
Entendiendo la fórmula ABC
La fórmula abc es una de las fórmulas que se utilizan para encontrar las raíces de una ecuación cuadrática. Aquí hay una forma general de esta fórmula.

Las letras a, byc en la fórmula abc se llaman coeficientes. El coeficiente de x2 al cuadrado es a, el coeficiente de x es byc es el coeficiente de constante, generalmente denominado término constante o independiente.
La ecuación cuadrática es básicamente una ecuación matemática que forma la geometría curva de la parábola en el cuadrante xy.
El valor del coeficiente en la fórmula abc tiene los siguientes significados:
- a determina la prabola cóncava / convexa formada por la ecuación cuadrática. Si el valor de a> 0 entonces la parábola se abrirá hacia arriba. Sin embargo, si a <0, la parábola se abrirá hacia abajo.
- b determina la posición x del pico del parabol, o la simetría especular de la curva. La posición exacta del eje de simetría es -b / 2a de la ecuación cuadrática.
- c determina el punto de intersección de la función de la ecuación cuadrática parabólica formada en el eje y o cuando el valor x = 0.
Ejemplo de preguntas y discusión
Aquí hay algunos ejemplos de problemas de ecuaciones cuadráticas y su discusión con soluciones usando fórmulas de ecuaciones cuadráticas.
1. Resuelve las raíces de la ecuación cuadrática x2 + 7x + 10 = 0 usando la fórmula abc!
Responder:
Lea también: 7 funciones de las proteínas para el cuerpo [Explicación completa]tenga en cuenta que a = 1, b = 7 y c = 10
entonces, las raíces de la ecuación son:

Entonces, el producto de las raíces de la ecuación x2 + 7x + 10 = 0 es x = -2 o x = -5
2. Usando la fórmula abc, encuentre el conjunto de soluciones para x2 + 2x = 0
Responder:
dado que a = 1, b = 1, c = 0
entonces las raíces de la ecuación son las siguientes:

Por tanto, el producto de las raíces de la ecuación x2 + 2x = 0 es x1 = 0 y x2 = -2, por lo que el conjunto de soluciones es HP = {-2,0}
3. Encuentra el conjunto de raíces x en el problema x2 - 2x - 3 = 0 usando la fórmula abc
Responder:
dado que a = 1, b = 2, c = -3
entonces los resultados de las raíces de la ecuación son los siguientes:

Así, con x1 = -1 y x2 = -3, el conjunto de soluciones es HP = {-1,3}
4. Determina el resultado de la ecuación cuadrática x 2 + 12x + 32 = 0 usando la fórmula abc !
Responder:
tenga en cuenta que a = 1, b = 12 y c = 32
entonces las raíces de la ecuación son las siguientes:

Entonces, los resultados de las raíces de la ecuación cuadrática son -4 y -8
5. Encuentre el conjunto del siguiente problema 3x2 - x - 2 = 0
Responder:
tenga en cuenta que a = 3, b = -1, c = -2
entonces las raíces de la ecuación son las siguientes:

Por lo tanto, las raíces de la ecuación cuadrática 3x2 - x - 2 = 0 son x1 = 1 y x2 = -2 / 3, por lo que el conjunto de soluciones es HP = {1, -2 / 3}
6. Encuentra las raíces de la ecuación x 2 + 8x + 12 = 0 usando la fórmula abc!
Responder:
tenga en cuenta que a = 1, b = 8 y c = 12
entonces las raíces de la ecuación cuadrática son las siguientes:

Entonces, las raíces de la ecuación cuadrática x2 + 8x + 12 = 0 son x1 = -6 o x2 = -2 de modo que el conjunto de soluciones es HP = {-6, -2}
7. Resuelve las raíces de la ecuación x 2 - 6x - 7 = 0 con la fórmula abc .
Responder:
se sabe que a = 1, b = - 6 y c = - 7
entonces las raíces de la ecuación son las siguientes:
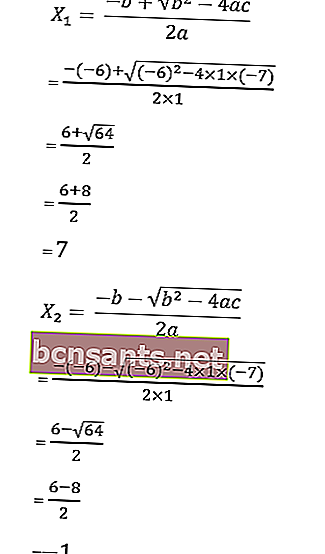
Entonces, las raíces son x 1 = 1 o x 2 = 5/2, por lo que el conjunto de soluciones es HP = {1, 5/2}.
Lea también: Ecuaciones cuadráticas (COMPLETO): definición, fórmulas, problemas de ejemplo8. Encuentra las raíces de la ecuación 2x 2 - 7x + 5 = 0 con la fórmula abc
Responder:
sabemos a = 2, b = - 7 y c = 5
entonces las raíces de la ecuación son las siguientes:
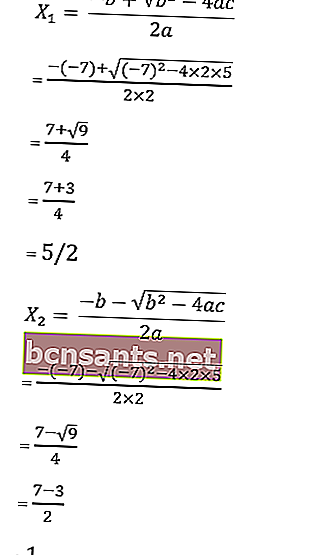
Entonces, las raíces son x1 = –4 o x2 = 5/3 de modo que el conjunto de soluciones es HP = {1, 5/3}.
9. Resuelve la ecuación 3x 2 + 7x - 20 = 0 con la fórmula abc.
Responder:
sabe que a = 3, b = 7 y c = - 20
entonces las raíces de la ecuación son:
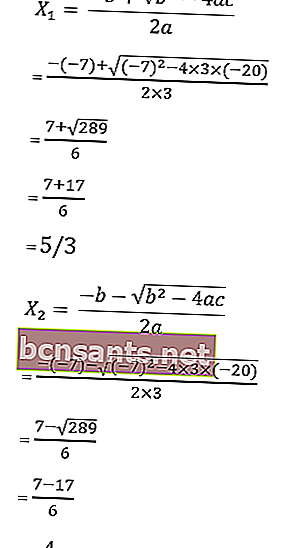
Entonces, las raíces son x1 = –4 o x2 = 5/3, por lo que el conjunto de soluciones es HP = {-4, 5/3}.
10. Encuentra las raíces de la ecuación 2x 2 + 3x +5 = 0 con la fórmula abc.
Responder:
sabemos que a = 2, b = 3 y c = 5
entonces las raíces de la ecuación son las siguientes:
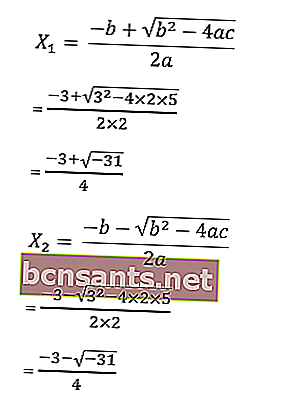
El resultado de la raíz de la ecuación 2x2 + 3x +5 = 0 tiene la raíz imaginaria √ - 31, por lo que la ecuación no tiene solución. El conjunto de soluciones se escribe como el conjunto vacío HP = {∅}
Esta es una explicación de la definición de la fórmula abc con ejemplos de preguntas y su discusión. ¡Puede ser útil!
