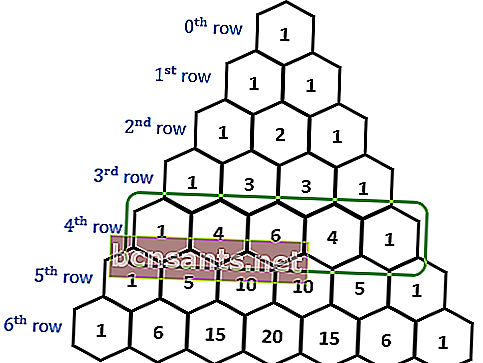
El triángulo de Pascal es un arreglo de triángulos creado sumando elementos adyacentes en la fila anterior. Esta disposición de triángulos se realiza agregando elementos adyacentes en la fila anterior.
Suponga que las variables ayb se suman y luego se elevan a la potencia de 0 a la potencia de 3, el resultado es la siguiente descripción.
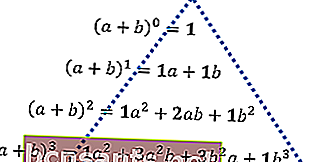
A continuación, considere la disposición de los números en negrita de arriba a abajo, hasta que encuentre una forma de triángulo. Este patrón numérico se denomina en lo sucesivo triángulo de Pascal.
Entendiendo el triángulo de Pascal
El triángulo de Pascal es la regla geométrica del coeficiente binomial en un triángulo.
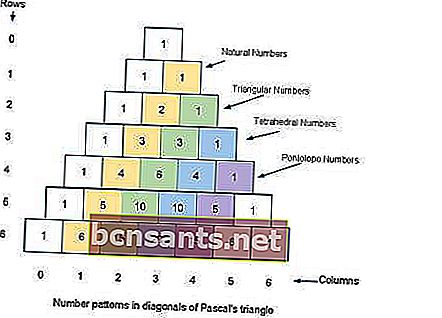
El triángulo lleva el nombre del matemático Blaise Pascal, aunque otros matemáticos lo estudiaron siglos antes que él en India, Persia, China e Italia.
Concepto de reglas
El concepto del triángulo de Pascal es un sistema de cálculo para este triángulo independientemente de las variables ay b. Esto significa que basta con prestar atención al coeficiente binomial, de la siguiente manera:
- En la línea cero, escriba solo el número 1.
- En cada fila a continuación, escriba el número 1 a la izquierda y a la derecha.
- La suma de los dos números de arriba, luego escrita en la línea de abajo.
- 1 a la izquierda y a la derecha según (2), siempre rodea el resultado (3)
- Los cálculos se pueden continuar con el mismo patrón.
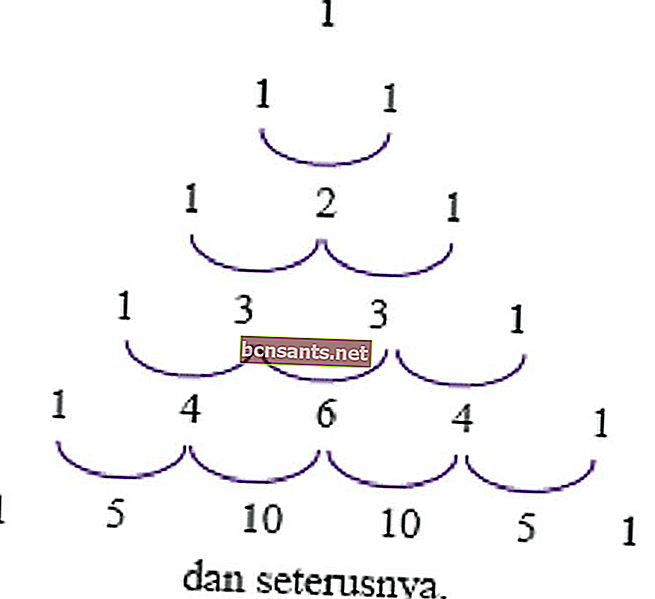

Un uso de este triángulo es determinar el coeficiente de potencia (a + b) o (ab) para hacerlo más eficiente. Este uso se describe en los siguientes ejemplos.
Ejemplo de problemas
Pista: preste atención al triángulo de Pascal.
1. ¿Cuál es la traslación (a + b) 4?
Solución : para (a + b) 4
- Primero, se ordenan las variables ayb, comenzando desde a4b o a4
- Entonces la potencia de a cae a 3, que es a3b1 (el total elevado a la potencia de ab debe ser 4)
- Luego, la potencia de a cae a 2, convirtiéndose en a2b2
- Luego, el poder de a cae a 1, convirtiéndose en ab3
- Entonces la potencia de a cae a 0, a b4
- A continuación, escriba la ecuación con el coeficiente delante del espacio en blanco.
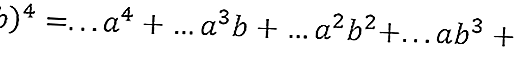
Según la Figura 2 en el 4o orden, se obtienen los números 1,4,6,4,1, por lo que se obtiene la traducción (a + b) 4

2. ¿Cuál es el coeficiente a3b3 en (a + b) 6?
Lea también: Material de campo magnético: fórmulas, problemas de ejemplo y explicacionesSolucion :
Basado en la pregunta número 1, el orden de las variables de (a + b) 6 se organiza, a saber
a6, a5b1, a4b2, a 3 b 3 .
Esto significa que en el cuarto orden (imagen 2, secuencia 6) en el patrón 1, 6, 15, 20 es 20 . Por tanto, se pueden escribir 20 a3b3.
3. Determine la traslación de (3a + 2b) 3
Asentamiento
La fórmula general para el triángulo pascal como la suma de las variables ayb elevadas a 3 se presenta de la siguiente manera

Al cambiar las variables a 3a y 2b, obtenemos

