
La construcción de espacio es un tema que se discute a menudo en matemáticas, la fórmula es a menudo un problema de matemáticas en los niveles de primaria y secundaria.
El espacio del edificio se puede interpretar como un edificio que matemáticamente tiene volumen o contenido. También se puede interpretar que la forma de un espacio es una forma tridimensional que tiene volumen o espacio y está limitada por lados.
Hay varias formas de espacio en sí, como bloques, cubos, tubos, bolas, etc.
Cada una de estas formas tiene una fórmula de volumen y área de superficie respectivamente. Esto a veces dificulta que muchos estudiantes recuerden.
Aquí hice una lista completa de fórmulas de construcción, para que pueda resolver fácilmente varios problemas matemáticos sobre este tema.
1. Cubo
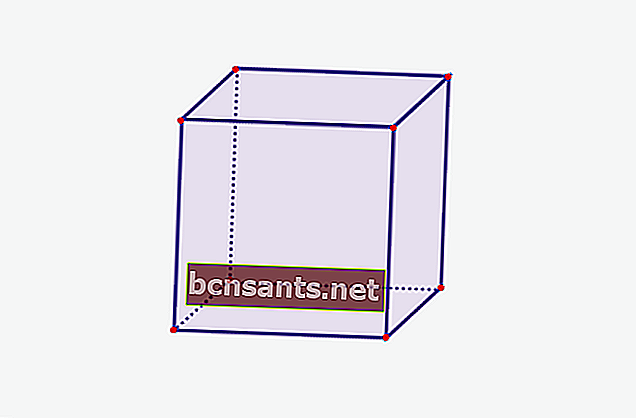
| Volumen del cubo | V = sxsxs |
| El área de la superficie del cubo | L = 6 x (sxs) |
| Encierra en un círculo el cubo | K = 12 xs |
| Área de un lado | L = sxs |
2. Vigas
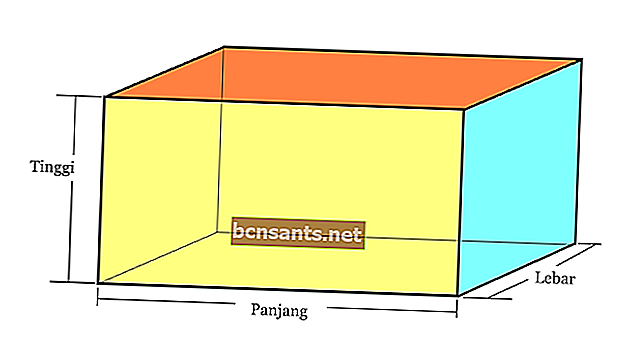
| Volumen de bloque | V = pxlxt |
| Área de superficie del bloque | L = 2 x (pl + lt + pt) |
| Espacio diagonal | d = √ ( p2 + l2 + t2) |
| La circunferencia de la viga | K = 4 x (w + l + h) |
3. Prisma triangular
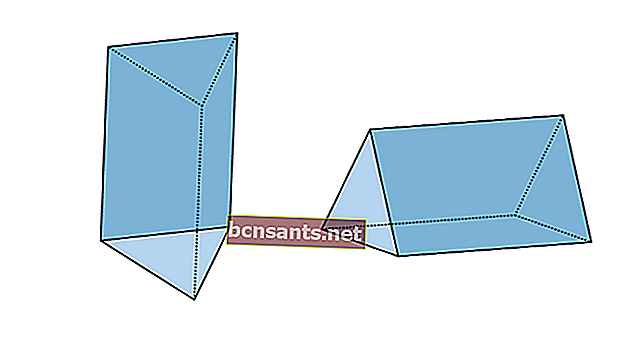
| El volumen del prisma triangular. | V = área de la base xt |
| El área de la superficie del prisma triangular | L = perímetro de la base xt + 2 x área de la base del triángulo |
4. Quinto cuadrilátero
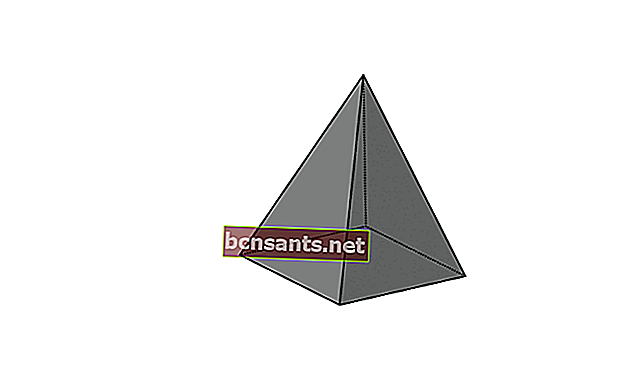
| El volumen de la pirámide | V = 1/3 xpxlxt |
| El área de la superficie de la pirámide. | L = área de la base + área de la carcasa piramidal |
5. Quinto triángulo
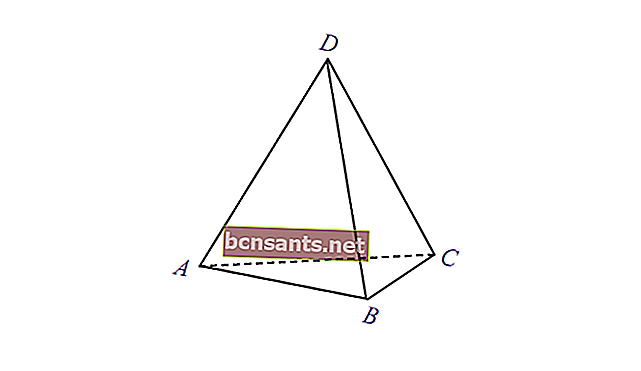
| El volumen de la pirámide | V = 1/3 x área de la base xt |
| Área de superficie | L = área de la base + área de la carcasa piramidal |
6. Tubos

| Volumen del tubo | V = π x r2 xt |
| Área de superficie del tubo | L = (2 x área de la base) + (perímetro de la base x altura) |
7. Conos

| Volumen del cono | V = 1/3 x π x r2 xt |
| El área de la superficie del cono | A = (π x r2) + (π xrxs) |
bola 8

| Volumen de bola | V = 4/3 x π x r3 |
| La superficie de la pelota | A = 4 x π x r2 |
Tabla completa de fórmulas de construcción
También puede obtener la lista anterior brevemente mirando la tabla a continuación. También puede guardar esta imagen para poder volver a verla en cualquier momento.
Esta es una explicación de la fórmula de la forma del edificio para calcular el volumen y la superficie.
Con suerte, la explicación anterior puede ayudarlo a comprender la forma del espacio, para que pueda usarlo para resolver problemas matemáticos y sus diversas aplicaciones en la vida cotidiana.
Referencia
- Revisión de fórmulas de volumen - Khan Academy
- Hoja de fórmulas de geometría
