
La fórmula de la desviación estándar o lo que se conoce como la desviación estándar es una técnica estadística que se utiliza para explicar la homogeneidad de un grupo.
La desviación estándar se puede utilizar también para explicar cómo los datos se distribuyen en una muestra, así como la relación entre los puntos individuales y la media de valor o promedio de la muestra.
Antes de seguir discutiendo, hay algunas cosas que debemos saber primero, a saber dónde:
La desviación estándar del conjunto de datos puede ser cero, mayor o menor que cero.
Estos valores variables tienen significados, a saber:
- Si la desviación estándar es cero, entonces todos los valores de muestra en el conjunto de datos son iguales.
- Mientras tanto, el valor de la desviación estándar mayor o menor que cero indica que el punto de datos del individuo está lejos del valor promedio.

Pasos para encontrar la desviación estándar
Para determinar y encontrar el valor de desviación estándar, debemos seguir los pasos a continuación.
- El primer paso
Calcule el valor promedio o medio en cada punto de datos.
Para ello, suma cada valor en el conjunto de datos y luego el número se divide por el número total de puntos de los datos.
- El siguiente paso
Calcule la varianza de los datos calculando la desviación o la diferencia para cada punto de datos del valor promedio.
El valor de desviación en cada punto de datos se eleva al cuadrado y se elimina por el cuadrado del valor medio.
Después de obtener el valor de la varianza, podemos calcular la desviación estándar enraizando el valor de la varianza.
Lea también: Narración: definición, propósito, características, tipos y ejemplosFórmulas de desviación estándar
1. Desviación estándar de la población
Una población está simbolizada por σ (sigma) y se puede definir mediante la fórmula:

2. Desviación estándar de la muestra
La formula es:
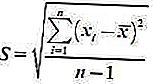
3. La fórmula para la desviación estándar de muchos grupos de datos
Para averiguar la distribución de datos de una muestra, podemos reducir cada valor de datos por el valor promedio, luego se suman todos los resultados.
Sin embargo, si usa el método anterior, el resultado siempre será cero, por lo que ese método no se puede usar.

Para que el resultado no sea cero (0), primero debemos elevar al cuadrado la resta del valor de los datos y el valor promedio, luego sumar todos los resultados.
Al usar este método, el resultado de la suma de cuadrados tendrá un valor positivo.

El valor de la varianza se obtendrá dividiendo la suma de cuadrados por el número de tamaños de datos (n).
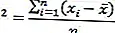
Sin embargo, si usamos este valor de variante para encontrar la varianza de la población, el valor de varianza será mayor que la variante de la muestra.
Para superar esto, el tamaño de los datos (n) como divisor debe reemplazarse con grados de libertad (n-1) para que el valor de la varianza de la muestra se acerque a la variante de la población.
Por lo tanto, la fórmula de la variante de muestra se puede escribir como:

El valor de la variante que se ha obtenido es el valor cuadrado, por lo que primero debemos elevarlo al cuadrado para obtener la desviación estándar.

Para facilitar el cálculo, la fórmula para la varianza y la desviación estándar se puede reducir a la siguiente fórmula.
Fórmulas de variantes de datos
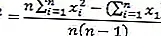
Fórmula de desviación estándar
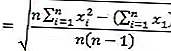
Observaciones :
s2 = variante
s = desviación estándar
x i = el iésimo valor de x
n = tamaño de la muestra
Ejemplo de problemas de desviación estándar
El siguiente es un ejemplo y trabaja en problemas de desviación estándar.
Pregunta:
Sandi, como presidente de los miembros extracurriculares, tiene la tarea de registrar la altura total de los miembros. Los datos que ha recopilado la contraseña son los siguientes:
167, 172, 170, 180, 160, 169, 170, 173, 165, 175
A partir de los datos anteriores, calcule la desviación estándar.
Lea también: Código Morse: Historia, fórmulas y métodos de memorizaciónRespuesta :
| yo | x yo | x yo 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
De los datos anteriores, se puede ver que el número de datos (n) = 10 y grados de libertad (n-1) = 9 también
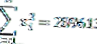
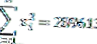
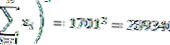
Para que podamos calcular el valor de la varianza de la siguiente manera:

El valor de la variante de los datos recopilados por Sandi es 30,32 . Para calcular la desviación estándar solo necesitamos elevar al cuadrado el valor de la varianza para que:
s = √30,32 = 5,51
Entonces, la desviación estándar del problema anterior es 5.51
Beneficios y aplicaciones
Los estadísticos suelen utilizar la desviación estándar para determinar si los datos obtenidos son representativos de toda la población.

Por ejemplo, alguien quiere saber el peso de un niño de 3 a 4 años en una aldea.
Entonces, para hacerlo más fácil, solo necesitamos averiguar el peso de algunos niños y luego calcular el promedio y la desviación estándar.
A partir de los valores de la desviación estándar y la media, podemos representar el peso corporal total de los niños de 3 a 4 años de una aldea.
Referencia
- Desviación estándar: fórmulas para encontrar y ejemplos de problemas
- Desviación estándar: fórmulas de cálculo y problemas de ejemplo
