
La fórmula de Pitágoras es la fórmula que se usa para encontrar una de las longitudes de los lados de un triángulo.
La fórmula de Pitágoras, también conocida como el teorema de Pitágoras, es una de las primeras materias de matemáticas enseñadas.
Desde la escuela primaria se nos ha enseñado esta fórmula pitagórica.
En este artículo, discutiré nuevamente la proposición del teorema de Pitágoras junto con ejemplos de problemas y sus soluciones.
Historia de Pitágoras - Pitágoras
De hecho, Pitágoras es el nombre de una persona de la época griega antigua entre el 570 y el 495 a. C.
Pitágoras fue un brillante filósofo y matemático de su época. Esto se evidencia en sus hallazgos que lograron resolver el problema de la longitud de los lados del triángulo con una fórmula muy simple.
Teorema de Pitágoras
El Teorema de Pitágoras es una proposición matemática sobre triángulos rectángulos, que muestra que la longitud de la base del cuadrado más la longitud de la altura del cuadrado es igual a la longitud de la hipotenusa del cuadrado.
Suponer….
- La longitud de la base del triángulo es un
- La longitud de la altura es b
- La longitud de la hipotenusa es c
Entonces, al usar el argumento de Pytaghoras, la relación entre los tres se puede formular como
a 2 + b 2 = c 2
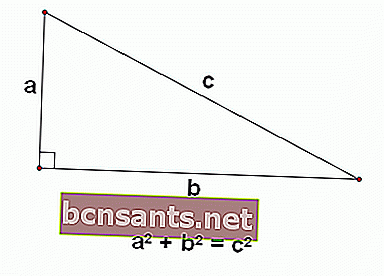
Prueba del teorema de Pitágoras
Si eres observador, podrás imaginar que básicamente la fórmula de las pitágoras muestra que el área de un cuadrado de lado a más el área de un cuadrado de lado b es igual al área de un cuadrado de lado c.
Puedes ver la ilustración en la siguiente imagen:

También puedes verlo en un video como el siguiente
Cómo utilizar la fórmula pitagórica
La fórmula fitgórica a 2 + b 2 = c 2 básicamente se puede expresar en varias formas, a saber:
a2 + b2 = c2
c2 = a 2 + b 2
a2 = c2 - b 2
b2 = c2 -a2
Para resolver cada una de estas fórmulas, puede utilizar el valor raíz de la fórmula pitagórica anterior.
Lea también: Microscopio: explicación, sus partes y función
Nota importante: no olvide que las fórmulas anteriores solo se aplican a triángulos rectángulos. Si no es así, no es válido.
Triple Pitágoras (patrón numérico)
Triple pitagórico es el nombre del patrón numérico abc que cumple con la fórmula pitagórica anterior.
Hay tantos números que llenan este triple pytaghoras, incluso hasta números muy grandes.
Algunos ejemplos incluyen:
- 3 - 4 - 5
- 5 - 12 - 13
- 6 - 8 - 10
- 7 - 24 - 25
- 8 - 15 - 17
- 9 - 12 - 15
- 10 - 24 - 26
- 12 - 16 - 20
- 14 - 48 - 50
- 15 - 20 - 25
- 15 - 36 - 39
- 16 - 30 - 34
- 17-144-145
- 19 - 180 - 181
- 20 - 21 - 29
- 20 - 99 - 101
- 21 - 220 - 221
- 23 - 264 - 265
- 24 –143-145
- 25 - 312 - 313
- etc
La lista todavía puede continuar hasta un gran número.
En esencia, los números coincidirán cuando coloque los valores en la fórmula a 2 + b 2 = c 2
Ejemplos de preguntas y discusiones completas
Para comprender mejor el tema de esta fórmula de Pytaghoras, veamos el ejemplo de la pregunta completa y su discusión a continuación.
Ejemplo de fórmula pitagórica 1
1. Un triángulo tiene un lado BC de 6 cm de largo y un lado AC de 8 cm , ¿cuántos cm es la hipotenusa del triángulo (AB)?
Asentamiento:
Conocido:
- BC = 6 cm
- CA = 8 cm
Se busca: ¿longitud AB?
Responder:
AB2 = BC2 + AC2
= 62 + 82
= 36 + 64
= 100
AB = √100
= 10
Por tanto, la longitud del lado AB (inclinado) es de 10 cm.
Ejemplo del teorema de Pitágoras 2
2. Se sabe que un triángulo tiene una hipotenusa de 25 cm de largo y el lado vertical del triángulo tiene una longitud de 20 cm . ¿Cuál es la longitud del lado plano?
Asentamiento:
Se sabe: ponemos un ejemplo, para que sea más fácil
- c = hipotenusa, b = lado plano, a = lado vertical
- c = 25 cm, a = 20 cm
Se busca: ¿La longitud del lado plano (b)?
Responder:
b2 = c2 - a2
= 252 - 202
= 625 - 400
= 225
b = √225
= 15 cm
De modo que la longitud del lado plano del triángulo sea de 15 cm .
Ejemplo de fórmula pitagórica 3
3. ¿Cuál es la longitud del lado vertical de un triángulo si sabes que la hipotenusa del triángulo es de 20 cm y el lado plano tiene una longitud de 16 cm ?
Solucion :
Se sabe: primero hacemos el ejemplo y el valor
- c = hipotenusa, b = lado plano, a = lado vertical
- c = 20 cm , b = 16 cm
Se busca: ¿La longitud de la vertical (a)?
Responder:
a2 = c2 - b2
= 202 - 162
= 400 - 256
= 144
a = √144
= 12 cm
De esto, obtienes que la longitud del lado del triángulo que está en posición vertical es de 12 cm .
Ejemplo del problema 4 de Triple Pitágoras
Continúe el valor del siguiente triple pitagórico….
3, 4,….
6, 8,….
5, 12,….
Asentamiento:
Al igual que las soluciones de los problemas anteriores, esta triple relación pitagórica se puede resolver mediante la fórmula c2 = a 2 + b 2.
Intente calcularlo usted mismo….
La respuesta (que debe coincidir) es:
- 5
- 10
- 13
Ejemplo de fórmulas de Pitágoras Problema 5
Dado que tres ciudades (A, B, C) forman un triángulo, con codos en la ciudad B.
Distancia a la ciudad AB = 6 km, distancia a la ciudad BC = 8 km, ¿cuál es la distancia a la ciudad AC?
Asentamiento:
Puede usar la fórmula del teorema de Pitágoras y obtener el resultado de calcular la distancia a la ciudad AC = 10 km.
De ahí la discusión de la fórmula de Pitágoras: los argumentos del teorema de Pitágoras, que se presenta simplemente. Ojalá puedas entenderlo bien, para que luego puedas entender otros temas matemáticos, como trigonometría, logaritmos, etc.
Si aún tiene preguntas, puede enviarlas directamente en la columna de comentarios.
Referencia
- ¿Cuál es la proposición de Pitágoras? - Preguntando hijo
- Teorema de Pitágoras: las matemáticas son divertidas
