
La integral indefinida o también conocida como anti-derivada es una forma de operación de integración que produce una nueva función .
Integral juega un papel muy importante en matemáticas. La teoría puede determinar el área bajo la curva de una función.
Integral es útil para el límite de suma que es continuo sobre una función continua. Integral es anti-derivado. Entonces, si f es una función continua, entonces el resultado integral de la función f se denota como F.
Los tipos integrados basados en ciertos límites funcionales no son seguros. La siguiente es una discusión para los tipos de integrales con límites indefinidos.
Integral indefinida
Una integral indefinida o también conocida como anti-derivada o anti-desinversión es una forma de operación de integración que produce una nueva función.
Considere la siguiente ecuación.

con C una constante. La fórmula integral indefinida es la siguiente
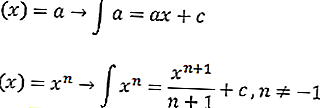
o igual a

con
- a (x) ^ n = Función de ecuación
- a = constante
- x = variable
- n = Potencia de la función de la ecuación
- C = constante
El resultado de esta integral indefinida es una función que es una nueva función que no tiene un valor determinado o definido porque todavía hay variables en la nueva función.
Para que pueda comprender mejor el concepto de integral indeterminada, considere el problema de ejemplo a continuación.

Con base en este ejemplo, se puede formular una operación integral, a saber
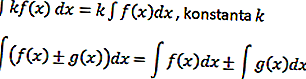
Integral trigonométrica
La integral de una función no es necesariamente una constante, lineal o polinomial. En esta solución intergal, a menudo involucra elementos trigonométricos.
En la función trigonómica, también se aplican las definiciones de integrales que se organizan en la siguiente tabla.
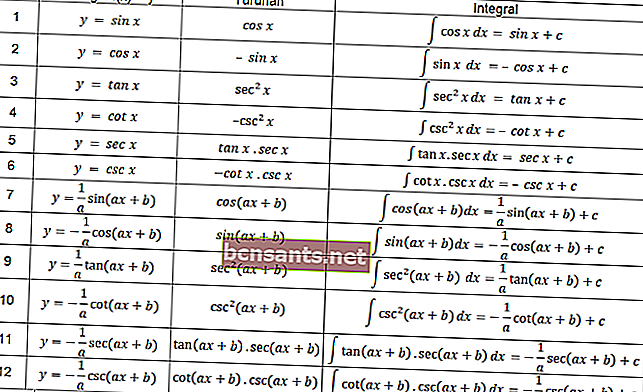
Puedes usar las ecuaciones de la tabla anterior para resolver el problema integral que involucra trigonometría.
Para comprender mejor las integrales trigonométricas, puede comprender los siguientes ejemplos
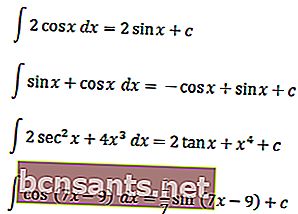
Esa fue la explicación de integrales indeterminadas en funciones trigonométricas ordinarias y especiales. Ojalá se pueda estudiar bien.
Lea también: Las normas de la decencia: definición, finalidad, sanciones y ejemplos [COMPLETO]Para comprender mejor el concepto de esta integral, puedes practicar haciendo preguntas de práctica. Si hay algo que quieras preguntar, escríbelo en la columna de comentarios.
