
La ecuación del círculo tiene la forma general x ^ 2 + y ^ 2 + Ax + By + C = 0, que se puede usar para determinar el radio y el centro de un círculo.
La ecuación circular que aprenderá a continuación tiene varias formas. En diferentes casos, la ecuación puede ser diferente. Por tanto, entiéndelo bien para que puedas memorizarlo de memoria.
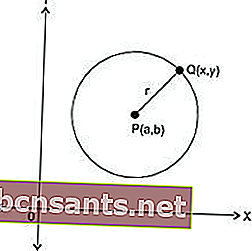
El círculo es un conjunto de puntos equidistantes de un punto. Las coordenadas de estos puntos están determinadas por la disposición de la ecuación. Esto se determina en función de la longitud del radio y las coordenadas del centro del círculo.
Ecuaciones circulares
Hay varios tipos de ecuaciones, a saber, ecuaciones formadas a partir del punto central y el radio y una ecuación que se puede encontrar para el punto central y el radio.
Ecuación del círculo general
Hay una ecuación general, como se muestra a continuación:
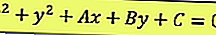
A juzgar por la ecuación anterior, se pueden determinar el punto central y el radio, son:
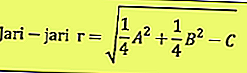
El centro del círculo es:
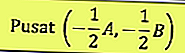
En el centro de P (a, b) y radio r
De un círculo, si conoce el punto central y el radio, obtendrá la fórmula:
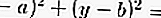
Si conoce el punto central de un círculo y el radio del círculo donde (a, b) es el centro y r es el radio del círculo.
A partir de la ecuación obtenida anteriormente, podemos determinar si los puntos incluidos se encuentran en el círculo, dentro o fuera. Para determinar la ubicación del punto, utilice la sustitución de puntos en las variables xey y luego compare los resultados con el cuadrado del radio del círculo.
Un punto M (x 1 , y 1 ) se encuentra:
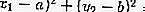
En el circulo:
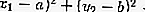
Dentro del círculo:
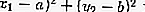
Fuera del círculo:
En con centro O (0,0) y radio r
Si el punto central está en O (0,0), haga la sustitución en la parte anterior, a saber:
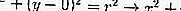
A partir de la ecuación anterior, se puede determinar la ubicación de un punto en el círculo.
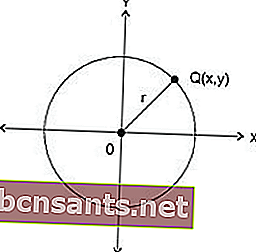
Un punto M (x 1 , y 1 ) se encuentra:
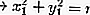
En el circulo:
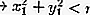
Dentro del círculo:
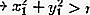
Fuera del círculo: Lea también: El arte es: definición, función, tipos y ejemplos [COMPLETO]
La forma general de la ecuación se puede expresar de las siguientes formas.
(x - a) 2 + (y - b) 2 = r2, o
X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0, o
X2 + y2 + Px + Qy + S = 0, donde P = -2a, Q = -2b y S = a2 + b2 - r2
La intersección de líneas y círculos
Un círculo con la ecuación x2 + y2 + Ax + By + C = 0 se puede determinar si una línea h con la ecuación y = mx + n no la toca, ofende o cruza usando el principio discriminante.
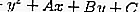
……. (ecuación 1)
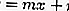
…… .. (ecuación 2)
Al sustituir la ecuación 2 por la ecuación 1, obtendrá una ecuación cuadrática, a saber:
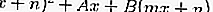
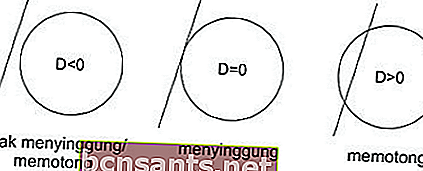
De la ecuación cuadrática anterior, al comparar los valores discriminantes, se puede ver si la línea no ofende / corta, ofende o interseca el círculo.
La línea h no cruza / ofende al círculo, entonces D <0
La recta h es tangente al círculo, entonces D = 0
La línea h interseca al círculo, entonces D> 0
Ecuaciones de tangentes a círculos
1. Ecuación de tangentes a través de un punto del círculo.
Las tangentes a un círculo se encuentran exactamente con un punto ubicado en el círculo. Desde el punto de intersección de la tangente y el círculo, se puede determinar la ecuación de la recta de la tangente.
La ecuación para la tangente al círculo que pasa por el punto P (x 1 , y 1 ), se puede determinar, a saber:
- Forma
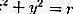
La ecuación de la tangente
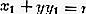
- Forma
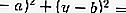
La ecuación de la tangente
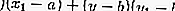
- Forma
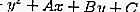
La ecuación de la tangente
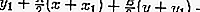
Ejemplo de problemas:
La ecuación para la tangente que pasa por el punto (-1,1) en el círculo
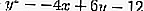
son:
Responder:
Conoce la ecuación del círculo
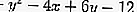
donde A = -4, B = 6 y C = -12 y x 1 = -1, y 1 = 1
PGS es
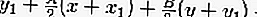
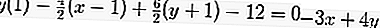
Entonces la ecuación de la tangente es
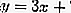
2. La ecuación es tangente al gradiente
Si una línea con pendiente m es tangente a un círculo,
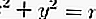
entonces la ecuación de la tangente es:
Si es un circulo
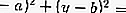
luego la ecuación de la tangente:

Si es un circulo
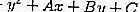
luego la ecuación de la tangente sustituyendo r con,
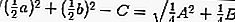
así que eso:
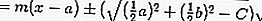
o
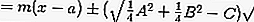
3. Ecuaciones de tangentes a puntos fuera del círculo
Desde un punto fuera del círculo, se pueden dibujar dos tangentes al círculo.
Lea también: Democracia: definición, historia y tipos [COMPLETO]Para encontrar la ecuación de la tangente, se usa la fórmula de la ecuación de línea regular, a saber:
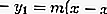
Sin embargo, a partir de esta fórmula, se desconoce el valor de la pendiente de la línea. Para encontrar la pendiente de la línea, sustituya la ecuación por la ecuación del círculo. Dado que la recta es tangente, a partir de la ecuación, la sustitución resulta para el valor D = 0, y se obtendrá el valor de m
Ejemplo de problemas
Problema de ejemplo 1
Un círculo tiene un punto central (2, 3) y tiene 8 cm de diámetro. La ecuación del círculo es ...
Discusión:
Como d = 8 significa r = 8/2 = 4, entonces la ecuación para el círculo que se forma es
(x - 2) ² + (y - 3) ² = 42
x² - 4x + 4 + y² -6y + 9 = 16
x² + y² - 4x - 6y - 3 = 0
Problema de ejemplo 2
Encuentre la ecuación general para el círculo centrado en el punto (5,1) y que ofende la línea 3 x - 4 y + 4 = 0!
Discusión:
Si se sabe que el centro del círculo ( a , b ) = (5,1) y la tangente al círculo es 3 x - 4 y + 4 = 0, entonces el radio del círculo se formula de la siguiente manera.
Por tanto, la ecuación general del círculo es la siguiente.
Por lo tanto, la ecuación general para un círculo centrado en (5,1) y que ofende la línea 3 x - 4 y + 4 = 0 es
Problema de ejemplo 3
¡Encuentre la ecuación general para un círculo centrado en (-3,4) y que ofenda el eje Y!
Discusión:
En primer lugar, dibujemos primero el gráfico del círculo, que está centrado en (-3,4) y ofende al eje Y.
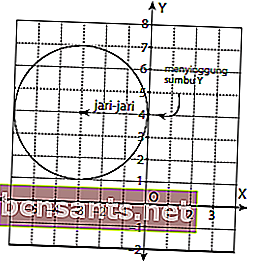
Basado en la imagen de arriba, se puede ver que el centro del círculo está en la coordenada (-3,4) con un radio de 3, por lo que:
Por tanto, la ecuación general que se centra en (-3,4) y ofende al eje Y es
En algunos casos, no se conoce el radio del círculo, pero se conoce la tangente. Entonces, ¿cómo determinar el radio del círculo? Mira la siguiente imagen.
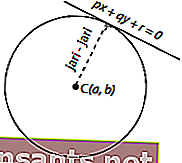
La imagen de arriba muestra que la tangente a la ecuación px + qy + r = 0 pertenece al círculo centrado en C ( a, b ). El radio se puede determinar mediante la siguiente ecuación. a, b ). El radio se puede determinar mediante la siguiente ecuación.

Puede ser útil.
