
La fórmula de un triángulo para encontrar el área de la forma es 1/2 x base x altura, para encontrar el perímetro del triángulo se puede encontrar sumando las longitudes de cada lado del triángulo.
En Matemáticas, se nos enseña sobre varias formas. Uno de ellos tiene forma de triángulo. La forma triangular es la forma más simple entre los distintos tipos de formas.
Un triángulo está formado por tres lados con tres ángulos delimitados por un segmento. Además, el ángulo total del triángulo es de 180 grados.
Hay varios tipos de triángulos. Según la longitud de los lados, hay triángulos equiláteros con longitudes de lados iguales, triángulos isósceles con dos lados iguales de catetos y cualquier triángulo con longitudes diferentes de tres lados.
Mientras tanto, según el ángulo, hay un triángulo agudo con un ángulo de menos de 90 grados, un triángulo obtuso con un ángulo de más de 90 grados y un triángulo rectángulo con un ángulo de 90 grados.
Con respecto a los triángulos, hay varios componentes que deben conocerse, incluido el área y el perímetro del triángulo. La siguiente es una explicación del área y el perímetro del triángulo junto con un ejemplo del problema.
Área del triángulo

El área, el área o el área es una cantidad que expresa el tamaño bidimensional, es decir, una parte de la superficie claramente definida por una curva o línea cerrada.
El área del triángulo es el tamaño del propio triángulo. La siguiente es la fórmula para el área de un triángulo:
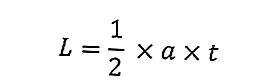
donde L es el área del triángulo (cm 2 ), a es la base del triángulo (cm) y h es la altura del triángulo (cm).
Ejemplo de problema del área de un triángulo
Problema de ejemplo 1
Hay un triángulo agudo cuya longitud de base es a = 10 cm y también tiene una altura de h = 8 cm. Calcula el área del triángulo.
Lea también: Animales: características, tipos, ejemplos [explicación COMPLETA]Solución:
Si: a = 10 cm, h = 8 cm
Se busca: ¿El área del triángulo?
Responder:
L = ½ xaxt
= ½ x 10 x 8
= 40 cm2
Entonces, el área del triángulo agudo es 40 cm2
Problema de ejemplo 2
Un triángulo rectángulo tiene una base de 15 cm y una altura de 20 cm. Encuentra y calcula el área del triángulo rectángulo.
Solución:
Si: a = 15 cm, h = 20 cm
Se busca: ¿El área del triángulo?
Responder:
L = ½ xaxt
= ½ x 15 x 20
= 150 cm2
Entonces, el área del triángulo rectángulo es 150 cm2
Problema de ejemplo 3
Un triángulo obtuso con una base de 8 cm y una altura de 3 cm, entonces, ¿cuál es el área del triángulo?
Solución:
Si: a = 8 cm, h = 3 cm
Se busca: ¿El área del triángulo?
Responder:
L = ½ xaxt
= ½ x 8 x 3
= 12 cm2
Entonces, el área del triángulo obtuso es 12 cm2
Problema de ejemplo 4
Un triángulo isósceles con la misma longitud de lado mide 13 cm y la base del triángulo mide 10 cm. ¿Cuál es el área del triángulo isósceles?
Solución:
Ya sabes: s = 13 cm, a = 10 cm
Se busca: ¿El área del triángulo?
Responder:
La altura del triángulo no se conoce, por lo que usamos la fórmula de Pitágoras para encontrar la altura del triángulo:

Dado que se conoce la altura del triángulo, entonces:
L = ½ xaxt
= ½ x 10 x 12
= 60 cm2
Entonces, el área del triángulo isósceles es 60 cm2
Perímetro del triángulo

El perímetro es el número de lados en una forma bidimensional. Entonces, el perímetro del triángulo es la suma de los lados del triángulo mismo.
Aquí está la fórmula para el perímetro de un triángulo:
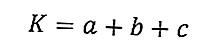
donde K es el perímetro del triángulo (cm) y a, b, c son las longitudes de los lados del triángulo (cm).
Ejemplo de perímetro de un triángulo
Problema de ejemplo 1
Un triángulo equilátero tiene lados que miden 15 cm de largo. ¿Cuál es el perímetro del triángulo?
Solución:
Ya sabes: largo de lado = 15 cm
Pregunta: ¿ circunferencia =….?
Responder:
K = lado a + lado b + lado c
debido a que es un triángulo equilátero, las longitudes de los tres lados son iguales.
K = 15 + 15 + 15
= 45 cm
Entonces , el perímetro del triángulo equilátero es de 45 cm.
Lea también: La interacción social es: definición y explicación completasProblema de ejemplo 2
Un triángulo arbitrario tiene lados de 3 cm, 5 cm y 8 cm. Calcula el perímetro del triángulo.
Solución:
Ya sabes: a = 3 cm, b = 5 cm yc = 8 cm
Pregunta: ¿circunferencia =….?
Responder:
K = lado a + lado b + lado c
= 3 + 5 + 8
= 16 cm
Entonces, el perímetro del triángulo es de 16 cm.
Problema de ejemplo 3
Un triángulo isósceles tiene lados iguales a 10 cm y una base de 6 cm. Calcula el perímetro del triángulo isósceles.
Solución:
Sabes que los lados miden 10 cm de largo y 6 cm de largo
Pregunta: ¿ circunferencia =….?
Responder:
K = lado a + lado b + lado c
debido a que el triángulo es isósceles, entonces hay dos lados que tienen la misma longitud, es decir, 10 cm, luego K = 10 + 10 + 6 = 26 cm
Entonces, el perímetro del triángulo isósceles es 26 cm
Problema de ejemplo 4
Un triángulo isósceles tiene una altura de 8 cm y una base de 12 cm. Calcula el perímetro del triángulo.
Solución:
Ya sabes: la altura del triángulo h = 8 cm
lado de la base a = 12 cm
Pregunta : ¿ circunferencia =….?
Responder:
K = lado a + lado b + lado c
Los dos lados del triángulo son desconocidos, así que usamos la fórmula de Pitágoras para encontrar la longitud de ese lado.

K = 10 + 10 + 12
K = 32 cm
Entonces, el perímetro del triángulo isósceles es 32 cm
Esta es una explicación del área de un triángulo y el perímetro del triángulo junto con ejemplos y discusión. Puede ser útil.
