
El valor absoluto en cálculo es muy útil para resolver varios problemas matemáticos, tanto en ecuaciones como en desigualdades. La siguiente es una explicación completa de valores absolutos y ejemplos de preguntas.
Definición de valor absoluto
Todos los números tienen sus respectivos valores absolutos. Todos los números absolutos son positivos, por lo que los valores de números absolutos de los números con el mismo número pero la diferencia entre las notaciones positivas (+) y negativas (-) tendrán el mismo resultado de número absoluto.
Si x es miembro de un número real, entonces el valor absoluto se escribe como | x | y se define como sigue:

"El valor absoluto es un número con el mismo valor de longitud o distancia desde el origen o punto cero en las coordenadas".
Se puede interpretar que el valor absoluto de 5 es la longitud o distancia del punto 0 al punto 5 o (-5).
Los valores absolutos de (-9) y 9 son 9. Los valores absolutos de 0 son 0, y así sucesivamente. Nilaa
Lo entenderé absolutamente mirando la siguiente imagen:

En la imagen de arriba, se puede entender que el valor de | 5 | es la distancia del punto 5 al número 0, es decir, 5, y | -5 | la distancia del punto (-5) desde el número 0 es 5.
Si | x | representa la distancia desde el punto xa 0, luego | xa | es la distancia del punto x al punto a. Por ejemplo, al expresar la distancia del punto 5 al punto 2, se podría escribir como | 5-2 | = 3

En general, se puede afirmar que la distancia xa se puede escribir con la notación | xa | o | hacha |
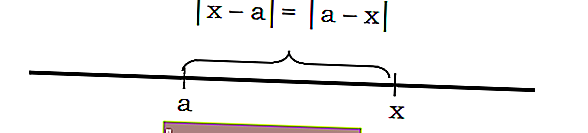
Por ejemplo, la distancia de un número al punto 3 vale 7 de la siguiente manera:
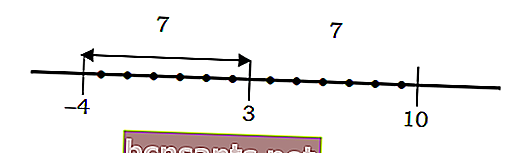
Si se describe en la ecuación algebraica | x-3 | = 7, se puede resolver de la siguiente manera:
Lea también: Medición de terremotos con logaritmos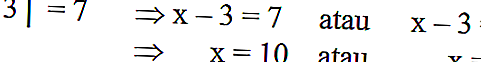
Recuerde que | x-3 | es la distancia del número x al punto 3, donde | x-3 | = 7 es la distancia del número x al punto 3 para 7 unidades.
Propiedades del valor absoluto
En las operaciones de ecuaciones de números absolutos, existen propiedades de números absolutos que pueden ayudar a resolver ecuaciones de números absolutos.
A continuación se muestran las propiedades de los números absolutos en general en ecuaciones de valor absoluto:

Las propiedades del valor absoluto de la desigualdad:
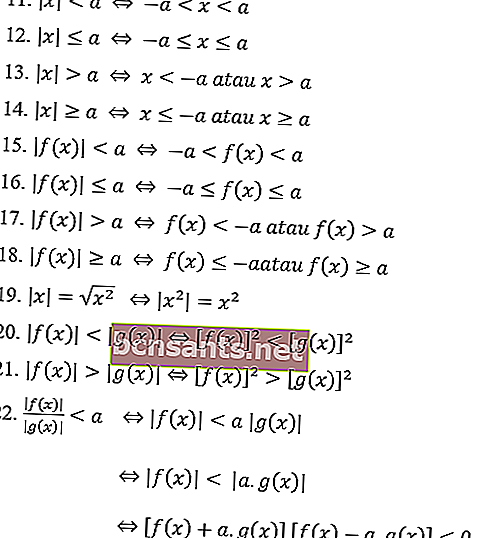
Ejemplos de problemas de ecuaciones de valor absoluto
Problema de ejemplo 1
¿Cuál es el valor absoluto de la ecuación | 10-3 |?
Responder:
| 10-3 | = | 7 | = 7
Problema de ejemplo 2
¿Cuál es el resultado de x para la ecuación para el valor absoluto | x-6 | = 10?
Responder:
Para resolver esta ecuación, hay dos resultados posibles para números absolutos
| x-6 | = 10
Primera solución:
x-6 = 10
x = 16
segunda solución:
x - 6 = -10
x = -4
Entonces, la respuesta a esta ecuación es 16 o (-4)
Problema de ejemplo 3
Resuelve y calcula el valor de x en la siguiente ecuación
–3 | x - 7 | + 2 = –13
Responder:
–3 | x - 7 | + 2 = –13
–3 | x - 7 | = –13 - 2
–3 | x - 7 | = –15
| x - 7 | = –15 / –3
| x - 7 | = 5
Hecho hasta la solución anterior, entonces el valor x tiene dos valores
x - 7 = 5
x = 12
o
x - 7 = - 5
x = 2
entonces el valor final de x es 12 o 2
Problema de ejemplo 4
Resuelve la siguiente ecuación y cuál es el valor de x
| 7 - 2x | - 11 = 14
Responder:
| 7 - 2x | - 11 = 14
| 7 - 2x | = 14 + 11
| 7 - 2x | = 25
Después de completar la ecuación anterior, los números para el valor absoluto de x son los siguientes
7 - 2x = 25
2x = - 18
x = - 9
o
7 - 2x = - 25
2x = 32
x = 16
Entonces el valor final de x es (- 9) o 16
Problema de ejemplo 5
Encuentre la solución a la siguiente ecuación de valor absoluto:
| 4x - 2 | = | x + 7 |
Responder:
Para resolver la ecuación anterior, use dos posibles soluciones, a saber:
Lea también: Errores en la lectura de los resultados estadísticos de la encuesta de elegibilidad de candidatos presidenciales4x - 2 = x + 7
x = 3
o
4x - 2 = - (x + 7)
x = - 1
Entonces, la solución para la ecuación | 4x - 2 | = | x + 7 | es x = 3 o x = - 1
Problema de ejemplo 6
Determine la solución de la siguiente ecuación de valor absoluto:
| 3x + 2 | ² + | 3x + 2 | - 2 = 0
¿Cual es el valor de x?
Responder:
Simplificación: | 3x + 2 | = p
entonces
| 3x + 2 | ² + | 3x + 2 | -2 = 0
p² + p - 2 = 0
(p + 2) (p - 1) = 0
p + 2 = 0
p = - 2 (el valor absoluto no es negativo)
o
p - 1 = 0
p = 1
| 3x + 2 | = 1
Hasta la solución anterior, hay 2 posibles respuestas para x, a saber:
3x + 2 = 1
3x = 1 - 2
3x = - 1
x = - 1/3
o
- (3x + 2) = 1
3x + 2 = - 1
3x = - 1 - 2
3x = - 3
x = - 1
Entonces, la solución a la ecuación es x = - 1/3 o x = - 1
Referencia: Valor absoluto: las matemáticas son divertidas
