
La fórmula para el perímetro es K = 2 × π × r, donde K = la circunferencia del círculo, π = la constante pi (3.14) y r = el radio del círculo. La siguiente es una explicación más completa acompañada de un problema de ejemplo.
La invención de la rueda es uno de los descubrimientos fundamentales sobre la importancia de las formas circulares en la vida cotidiana.
No solo ruedas, todavía hay muchas aplicaciones circulares si miramos a nuestro alrededor como neumáticos de coche, monedas, relojes de pared, piruletas, cintas de DVD, tapones de botellas, holahops y otros.

Bien, ¿no es tan importante esta forma de círculo? Obviamente muy importante. Entonces, aprendamos más sobre las fórmulas de círculo y círculo.
Construir un círculo
Un círculo es una forma bidimensional que consta de un conjunto de puntos que forman curvas / curvas que tienen la misma longitud en el centro del círculo. Aquí el punto P es el centro del círculo.
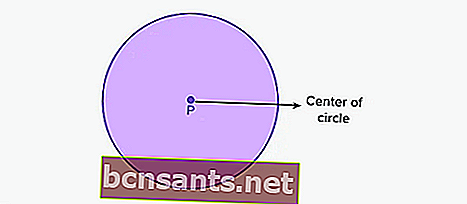
La misma longitud o distancia en todos los puntos desde el centro del círculo se llama radio del círculo . Mientras tanto, la distancia más larga que conecta los puntos exteriores de un círculo se llama diámetro del círculo.
Aparte del radio y el diámetro, un círculo tiene otros elementos como un círculo, un arco circular, un esqueleto y una cuerda.
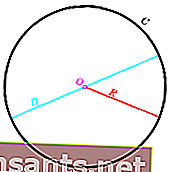
La forma de un círculo también tiene un área y una circunferencia. En la siguiente discusión nos enfocaremos solo en discutir la fórmula para la circunferencia de un círculo completo junto con un problema de ejemplo.
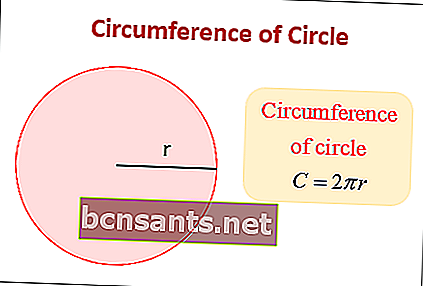
La fórmula de la circunferencia de un círculo.
La circunferencia de un círculo es la distancia desde un punto del círculo en un turno para volver al punto original. o también se puede interpretar como una medida de la longitud del círculo en sí.
Supongamos que tenemos un experimento, hay tres objetos diferentes que tienen forma circular. Luego medimos la circunferencia y el diámetro del círculo del objeto. Como se muestra en la siguiente tabla:
Por ejemplo, si tenemos una pulsera de metal. Luego, la pulsera se corta para formar una barra de metal recta, luego la longitud de la barra de metal es la circunferencia de la pulsera o la circunferencia del círculo.
| Cosa | Circunferencia (K) | Diámetro (d) | C / d = π |
| Lata de refresco | 24 cm | 7,7 cm | 3.11 |
| Latas de leche | 21,5 cm | 7,0 cm | 3,07 |
| Tupperware | 35,5 cm | 11 cm | 3,22 |
Después de eso, calculamos la relación entre la circunferencia y el diámetro y el promedio de las tres relaciones K / d del objeto es (3.11+ 3.07 +3.22) / 3 = 3.13.
Sí, la relación K / d siempre está cerca de 3,14 o 22/7. Esto significa que la relación entre la circunferencia de un círculo y el diámetro es constante o, a menudo, se denota por π (léase: phi).
Entonces, el valor de π = C / d = 3.14 o 22/7
Si ambos lados se multiplican por d, obtenemos,
C = π d
Información:
K = circunferencia del círculo
d = diámetro del círculo
π = 3,14 o 22/7
Dado que el diámetro es igual a 2 x el radio del círculo d = 2r, la circunferencia del círculo se convierte en,
C = πd = π.2r
C = 2 π r
Información:
K = circunferencia del círculo
r = el radio del círculo
π = 3,14 o 22/7
Problema de ejemplo con la fórmula de circunferencia
1. La circunferencia de un círculo es 396 cm. ¡Calcula el radio del círculo!
Conocido:
- K = 396 cm
Preguntó:
- r el radio del círculo?
Responder:
C = 2 π r
396 = 2 π r
396,7 = 2. 22/7. r
r = 2772/44
r = 63 cm
Entonces el radio del círculo es de 63 cm.
2. Encuentra la circunferencia de un círculo con un radio de 14 cm con π = 22/7
Conocido:
- r = 14 cm
- π = 22/7
Preguntó:
- ¿Cuál es la circunferencia del círculo?
Responder:
C = 2 π r
K = 2 x 22/7 x 14
K = 2 x 22 x 2
K = 88 cm
Entonces, la circunferencia del círculo es 88 cm.
3. Encuentra la circunferencia de un círculo con un diámetro de 10 cm con π = 3.14
Conocido:
- d = 10 cm
- π = 3,14
Preguntó:
¿Cuál es la circunferencia del círculo?
Responder:
C = π d
K = 3,14 x 10
K = 31,4 cm
Entonces la circunferencia del círculo es 31,4 cm.
4. ¡Calcula la circunferencia del área sombreada a continuación!
Conocido:
- r = 14 cm
Preguntó:
¿Alrededor del área sombreada?
Responder:
La imagen sobre la circunferencia consiste en la circunferencia de un cuadrado más la mitad del círculo y se resta por un semicírculo, con el mismo diámetro y lado del cuadrado, entonces la fórmula para la circunferencia se convierte en
Lea también: Los conductores son: descripciones, dibujos y ejemplosCircunferencia = 14 + 14 + ½ K + ½ K
= 14 + 14 + ½ π d + ½ π d
= 14 + 14 + ½. 22/7. 14 + ½. 22/7. 14
= 28 + 22+ 22
Circunferencia = 72 cm
Entonces, la circunferencia del área sombreada es igual a 72 cm.
5. Budi tiene una motocicleta que tiene ruedas con un diámetro de 84 cm y gira 1000 veces, calcula cuánta distancia ha recorrido el auto?
Conocido:
- d = 84 cm
- n = 1000 veces
Preguntó:
¿Hasta dónde cubre la moto?
Responder:
La distancia recorrida por el motor por 1000 veces la circunferencia del círculo = n / 2 = 1000/2 = 500
Entonces la distancia recorrida por el motor = 500x π d = 500.3,14. 84 = 131,880 cm = 1,31 km
6. ¿Cuál es la circunferencia del círculo si el diámetro es de 40 cm?
Responder:
- Perímetro = π xd
- = 3,14 x 40
- = 125,66
Entonces la circunferencia del círculo es 125,66 cm.
7. Calcular la circunferencia del círculo con un diámetro de 20 cm.
Asentamiento:
Conocido:
- d = 20 cm
- π = 3,14
Preguntado: ¿Alrededor del círculo?
Responder:
- Circunferencia = π × d
- Circunferencia = 3,14 × 20
- Circunferencia = 62,8 cm
Entonces, la circunferencia del círculo es 62,8 cm.
Esta es una explicación completa de las fórmulas completas para la circunferencia de un círculo junto con un problema de ejemplo. ¡Puede ser útil!
Referencia:
- Circunferencias del círculo - Khan Academy
- Cómo calcular las circunferencias de un círculo - wikihow
