
La serie aritmética es un patrón de números de serie en matemáticas, que tiene beneficios muy importantes de varias maneras.
Por ejemplo, cuando ahorras, todos los días dejas regularmente una asignación de cinco mil rupias, al día siguiente serán diez mil y así sucesivamente. Con el tiempo tu dinero aumenta, ¿verdad?
Bueno, este patrón de suma se llama serie aritmética.
Antes de discutir las secuencias aritméticas, primero debemos entender acerca de las secuencias aritméticas porque los patrones de suma obtenidos por secuencias aritméticas provienen de secuencias aritméticas.
Secuencias aritméticas
La secuencia aritmética (Un) es una secuencia de números que tiene un patrón fijo basado en operaciones de suma y resta.
La secuencia aritmética consta del primer término (U 1 ), el segundo término (U 2 ) y así sucesivamente hasta el n o el término n (Un).
Cada tribu tiene la misma diferencia o diferencia. La diferencia entre cada tribu es lo que se llama diferencia, simbolizada como b . El primer término U 1 también se simboliza como a .
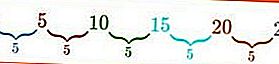
Secuencia aritmética: 0,5,10,15,20,25,…., Un
Por ejemplo, arriba hay una secuencia aritmética que tiene la misma diferencia, es decir, b = 5 y el primer término es a = 0. La diferencia se obtiene restando cada tribu. Por ejemplo, el segundo término U 2 menos el primer término U 1 , b = U 2 - U 1 = 5 - 0 = 5, el valor de b también se puede obtener del tercer término menos el segundo término y así sucesivamente, ¿no es fácil?
Ahora, para encontrar la fórmula del enésimo término (Un), podemos usar una fórmula práctica que es fácil de usar.

Donde, Un es el enésimo término, U n-1 es el término antes de n, a es el primer término , b es la diferencia yn es un número entero.
Para obtener más detalles sobre el material de la serie aritmética, considere las siguientes preguntas de muestra,
1. Dada una secuencia aritmética 3,7,11,15,…., Un. ¿Cuál es el décimo término de la línea U 10 anterior?
Lea también: Más de 25 mejores películas científicas recomendadas de todos los tiempos [ÚLTIMA ACTUALIZACIÓN]Discusión:
Se sabe por la secuencia anterior que el primer término a es 3, tiene una diferencia de b, es decir , 4 yn = 10.
¿Cuál es el décimo término de U 10 ? utilizando la fórmula anterior, U 10 se obtiene de la siguiente manera
U norte = a + (n-1) b
U 10 = 3 + (10-1) 4
= 3 + 36
= 39
Entonces, el décimo término en la secuencia aritmética anterior es 39
Progresión aritmética
Como se discutió anteriormente, la secuencia aritmética establece la secuencia de números U 1 , U 2 , ..., U n que tienen el mismo patrón. Mientras tanto, la secuencia aritmética es la suma de la disposición numérica en la secuencia aritmética U 1 + U 2 +… + Un al término n-.
El concepto real de esta serie aritmética es simple porque solo sumamos la secuencia aritmética que discutimos anteriormente al enésimo término, dependiendo de lo que esté ordenado.
Por ejemplo, agregamos la secuencia del problema de ejemplo anterior al cuarto término, ¿no es fácil? Pero, ¿qué pasa si sumas la secuencia aritmética hasta el término 100? Bueno, ¿cómo es que es tan difícil?
Por tanto, para facilitar el cálculo de esta serie aritmética, se utiliza una fórmula práctica
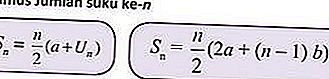
Con,
a es el primer término
b es diferente
Sn es el número del enésimo término
Ejemplo de problemas de series aritméticas
Dada una secuencia aritmética 3 + 7 + 11 + 15 +…. + Un. Determine el número del décimo término U 10 en la serie anterior
Discusión :
Se sabe que en la serie anterior a = 3, b = 4 yn = 10, se pregunta cuál es el número del décimo término de la serie anterior.
Usando una fórmula
Sn = n / 2 (2a + (n-1) b)
S 10 = 10/2 (2,3+ (10-1). 4)
= 5. (6 + 36)
= 210
Entonces, el número de la secuencia de los diez términos anteriores es 252
Entonces, ya comprende el material sobre series aritméticas, para ser aún más competente en el trabajo con problemas de series, considere las siguientes preguntas de muestra.
1. Hay una secuencia aritmética con los primeros 10 términos y el sexto término 20.
a. Determina la diferencia en la serie aritmética.
segundo. Escribe la secuencia aritmética.
C. Determina la suma de los primeros seis términos de la secuencia aritmética.
Lea también: La idea principal / idea principal es ... (Definición, tipos y características) COMPLETODiscusión :
Si a = 10 y U6 = 20,
a. Un = a + (n-1) b
U6 = a + (6-1) b
20 = 10+ (5) b
b = 10/5 = 2
segundo. Secuencia aritmética: 10 + 12 + 14 + 16 + 18 + 20 +… + Un
C. Número del sexto trimestre S6,
Sn = n / 2 (2a + (n-1) b)
S6 = 6/2 (2,10+ (6-1) 2)
= 3 (20 + 10)
= 90
Entonces, la suma del sexto término en la serie anterior es 90
2. Dada una secuencia aritmética: 2, 6, 10, 14, 18, ……… U n . Determina la fórmula para el enésimo término de la secuencia aritmética.
Discusión:
Dado que la línea aritmética anterior, a = 2 y b = 4, se solicita la fórmula para el enésimo término
Un = a + (n-1) b
Un = 2+ (n-1) 4
Un = 2 + 4n-4
Un = 4n-2
Entonces, la enésima fórmula para la fila de arriba es Un = 4n-2.
Ese es el material sobre series aritméticas, ¡espero que lo entiendas bien!
Referencia : Secuencia aritmética y suma: las matemáticas son divertidas
